Contoh Hasil Persamaan Simultan Gaus jordan, contoh 4.1 buku CFD

sesuai dengan contoh di buku CFD, saya mencoba menjalankan program yang sudah dibuat pada posting sebelumnya, langkah-langkah untuk menjalankan program tersebut adalah
1. masukkan nilai matrix nxn dan hasilnya pada kolom y, program ini mampu menghitung maksimal 250 persamaan.
2. masuk design mode geser letak button "mulai menghitung" agar tidak menganggu, keluar dari design mode, lalu klik button tersebut

3. setelah disusun seperti diatas, dan tombol mulai menghitung di klik akan muncul form seperti berikut

4. masukkan nilai matrix X terlebih dahulu, tinggal select range, seperti gambar dibawah berikut, hati-hati jangan sampai huruf X1,X2 dst ikut terselect

5. lanjutkan memilih untuk matrix hasil (Y)

6. lalu klik hitung, nilainya akan langsung muncul bersama dengan inversenya pada tab sheet baru dibawah bernama Hasil X! (lihat gambar dibawah ini)

7. hasilnya? alhamdulillah sama persis dengan di buku

file belum saya upload ke box tempat biasa saya sharing hasilnya, sesegera mungkin dech,

keep on touch

Read More

Persamaan Simultan, Bagaimana Penyelesaianya??

Metode Adjoint Matrix
persamaan simultan banyak sekali terdapat pada sistem engineering, dan ekonomi, terutama pada design termal, setiap input dan output menjadi satu varibel tertentu, sehingga semakin banyak input dan output pada suatu sistem, maka variabelnya juga semakin banyak. sehingga persamaan simultan mempunyai n persamaan dengan n variabel,secara persamaan dapat ditulis pada persamaan berikut

bila dinotasikan matrix tersebut dapat ditulis dengan bentuk sigma.. (gambar diatas paling bawah)
bila ditulis dalam bentuk matrix, dapat ditulis dengan

dapat kita lihat persyaratan utama untuk menyelesaikan matrix tersebut adalah untuk X yang tidak diketahui sejumlah n, maka persamaanya harus ada sejumlah n juga, hubungan antara koeffisien, X dan hasil (B) dapat ditulis dengan AX=B, sesuai dengan matrix diatas
dengan A adalah koeffisien matrix,
X adalah transpose matrix (X1,X2,X3....Xn), dan
B adalah tranpose matric (b1,b2,b3..bn)

dari hubungan AX=B, maka didapatkan

sedanngkan nilai dari

|A| adalah determinan dari matrix A, sehingga dari sini nilai A dapat dihitung dengan mudah.
metode ini adalah metode yang paling sering digunakan untuk proses perhitungan penyelesaian persamaan simultan, kenapa? karena kemudahannya dipakai untuk sampai 250 baris dan kolom. dan pemrogramanyapun cuman satu dan dapat dipakai berulang untuk matrix lainya.

Metode eliminasi Gaus
metode ini sudah pernah saya bahas diposting sebelumnya, yaitu metode eliminasi gaus, berserta contohnya
kekurangan metode ini adalah terdapat error bila nilai variabelnya tidak sesuai.

Metode Cramer
metode ini mengharuskan menghitung nilai determinant terlebih dahulu, baru setiap nilai dapat dihitung, sampai dengan tiga persamaan metode ini cukup mudah, namun untuk tiga persamaan lebih, metode ini cukup sulit digunakan untuk menghitung nilai determinan Ax lalu dibagi dengan determinan, pemrograman metode ini akan membuthkan lebih banyak waktu dibandingkan dengan metode gaus.

Contoh Program
contoh program yang saya buat berdasarkan beberapa literature VBA excel for engineer, silahkan check di posting disini

sebenarnya pembahasan untuk persamaan simultan masih panjang, misalnya untuk non homogen, augmented matrix dst. lebih lanjut silahkan check di refferensi berikut, dibaca di google book juga bisa kok

Metode Gauss Siedel
metode ini menggunakan sistem matrix dengan ketentuan sebagai berikut
AX=B

lalu nilai X dapat dihitung dengan rumus

dengan

Engineering Mathematics

 By V. P. Jaggi, A. B. Mathu

Read More

Penyelesaian persamaan simultan : alogaritma dan pemrograman visual basic (VBA) dan excel

persamaan simultan yang terdiri dari n persamaan dengan jumlah n yang tidak diketahui dapat diselesaikan dengan metode gaus jordan, untuk mempermudah digunakan prinsip matrik
Design form

seperti konsep sebelumnya untuk menampilkan form ini saya masukkan command button ke dalam excel langsung, seperti dibawah berikut, caranya aktifkan tabs developer lalu klik design mode, lalu insert command button, hasilnya seperti dibawah berikut

pada button tersebut masukkan perintah seperti berikut

Private Sub btn_Run_Gauss_Jordan_Click()

    frm_M_GaussJordan.Show

End Sub

perintah tersebut akan menampilkan form gausjordan (tergantung anda menamainya seperti apa)
Pembuatan Program
1. pemakaian input
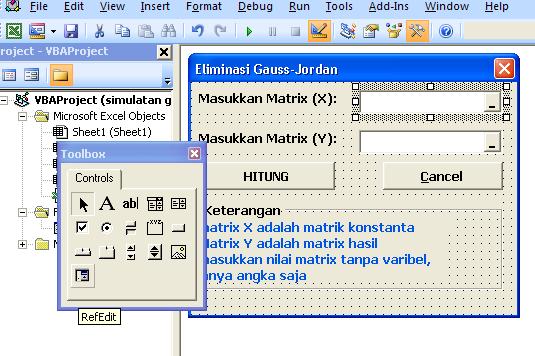
untuk memakai input saya memakai reference edit box, atau namanya refedit, tool ini hanya ada di VBA, penggunaanya adalah untuk menselect range(cell, cell) pada visual basic, untuk menghitung matrik, metode ini sangat efisien

cara memakainya tinggal masukkan ke form, dari toolbox, pilih refedit (pojok kiri bawah pada gambar diatas) hasilnya seperti pada box setelah masukkan matrix x...
2. membuat module program
membuat modul fungsi yang bisa dipanggil sudah saya jelaskan di beberapa posting sebelumnya, tentang bisection dan newton rapshon,
isi dari module tersebut kira-kira seperti ini, kata garis miring adalah keteranganya, biar mudah dipahami sesuai dengan permintaan sohib-sohib sekelas


Function Gauss_Jordan(A As Variant) As Variant
Dim i As Long, j As Long, k As Long, Atemp
Dim cols As Long, rows As Long, MaxVal As Double
Dim Max_Ind As Double, temp As Double, hold()


    'bila fungsi mulai dipanggil, jumlah kolom dan baris akan dihitung untuk menentukan jumlah n, dan apakah matrix yang ada dapat dihitung, object(A) maksudnya adalah matrix untuk X, = trus artinya bila ada nilainya
   
  If IsObject(A) = True Then
        cols = A.Columns.Count
        rows = A.rows.Count
    Else
        cols = UBound(A, 2)
        rows = UBound(A, 1)
    End If
    
    'menambahkan kolom untuk meletakkan hasil perhitungan,  Atemp merupakan matrix temporary sebelum digunakan nantinya dalam perhitungan.


    cols = cols + cols
    ReDim hold(1 To rows, 1 To cols), Atemp(1 To rows, 1 To cols)
    
    'menambahkan matrix x dan matrix y menjadi augmented matrix, aug matrix adalah matrix gabungan antara x dan y


    For i = 1 To rows
        For j = 1 To rows
            Atemp(i, j) = A(i, j)
            Atemp(i, j + rows) = 0#
        Next j
        Atemp(i, i + rows) = 1#
    Next i
    
    For i = 1 To rows
    
        MaxVal = Atemp(i, i)
        Max_Ind = i
       
 ' prosedure pendek menghitung nilai maximum, hal ini berguna untuk menentukan apakah matirx tersebut ada penyelesaianya atau tidak, akan muncul msg box error bila matrix ternyata singular


        For j = i + 1 To rows
            If Abs(Atemp(j, i)) > Abs(MaxVal) Then
                MaxVal = Atemp(j, i)
                Max_Ind = j
            End If
        Next j
        
        If MaxVal = 0 Then
            MsgBox Prompt:="Matrix adalah singular!", Title:="Error"
            Exit Function
        End If
        
        'prosedure perhitungan pivoting pada matrix


        For j = i To cols
            temp = Atemp(i, j)
                    Atemp(i, j) = Atemp(Max_Ind, j) / MaxVal
                      If Max_Ind <> i Then Atemp(Max_Ind, j) = temp
        Next j
        
        
        For k = 1 To rows
            If k <> i Then            
              
                For j = 1 To cols
                    hold(k, j) = -Atemp(k, i) * Atemp(i, j)
                Next j
             
                For j = 1 To cols
                   Atemp(k, j) = Atemp(k, j) + hold(k, j)
                Next j
            End If
        Next k
    Next i
    Gauss_Jordan = Atemp
End Function

------------------------------------------------------------------------
wahh.. panjang dan ribet? betul sekali, kok bisa bikin program seperti itu? nanti saya tunjukin rahasianya, sekarang kita teruskan membuat programnya

3. program pada button Hitung
double klik tombol hitung lalu masukkan perintah seperti berikut


Private Sub OK_Btn_Click()


Dim i As Double, j As Double, Data As Variant, n As Double
Dim A As Variant, MaxCol As Double, temp As Double, b()
Dim wks, cntsheets, newsheet As Worksheet, FinalCol As Double
Dim x(), Aplus(), Ainv()

' untuk menjaga agar inputan tidak salah, gunakan coding berikut ini, bila input matrix salah, atau ada huruf yang dimasukkan ke dalam cell, maka akan muncul peringatan kalau input matrix salah


If IP_A.Value = Empty Then
        Me.Hide
        MsgBox Prompt:="Pilih Cell untuk memasukkan angka." & vbCr & _
                       "Jangan tulis dengan variablenya.", _
                       Buttons:=48, Title:="Matrix input salah!"
        Me.Show
        Exit Sub
    End If

' matrix A adalah matrix input pada x


A = Application.RANGE(IP_A.Value)
 n = UBound(A, 1)

' pengecekan matrix untuk Y atau B pada program berikut


If IP_b.Value <> Empty Then
        b = Application.RANGE(IP_b.Value)
        If UBound(A, 1) <> UBound(b, 1) Then
            Me.Hide
            MsgBox Prompt:="baris di A harus sama dengan baris di b.", _
                   Buttons:=544, Title:="Error!"

     Err.Description = "Jumlah Baris Matrix tidak sama."
            GoTo EndProc
        End If
    End If

' terakhir menghitung inverse yang dilanjutkan untuk menghitung adjoint matrix, sehingga didapatkan nilai x1-xn

Aplus = Gauss_Jordan(A)
        If IsError(Aplus) Then GoTo EndProc
        ReDim Ainv(1 To n, 1 To n)
    For i = 1 To n
        For j = 1 To n
            Ainv(i, j) = Aplus(i, j + n)
        Next j
    Next i

If IP_b.Value <> Empty Then
        x = Application.MMult(Ainv, b)
    End If

' hasilnya diletakkan pada sheet baru


   cntsheets = Application.Sheets.Count - Application.Charts.Count
        Set newsheet = Application.Worksheets.add(after:=Worksheets(cntsheets))
        newsheet.name = "Hasil X!"
        FinalCol = 0


With Application
          .Cells(1, FinalCol + 1) = "Inverse Matrix "
        For j = 1 To n
           For i = 1 To n
               .Cells(i + 1, FinalCol + j).Value = Ainv(i, j)
           Next i
        Next j
        If IP_b.Value <> Empty Then
            FinalCol = FinalCol + n
            Cells(1, FinalCol + 1) = "SOLUSI"
            For i = 1 To n
                .Cells(i + 1, FinalCol + 1).Value = x(i, 1)
            Next i
        End If
    End With
    
    Application.Calculation = xlCalculationAutomatic


Unload Me
Exit Sub

-----------------
 program ini diambil dari beberapa sumber, ada tiga buku yang dipakai, satu buku berhasil saya download sedangkan dua buku lainya masih nongkrong di google book, silahkan check di refferensi bawah.

karena posting ini panjang, maka hasil programnya saya pisah, silahkan check dibawah ini, untuk mengetahui hasilnya, hasilnya dapat dilihat disini

Referensi Wajib

1.   Excel scientific and engineering cookbook  By David M. Bourg
2.   Numerical Methods with VBA Programming  By James Hiestand
3.   Excel for Scientists and Engineers: Numerical Methods   E. Joseph Billo 

Read More

Bisection : Alogaritma, pemograman menggunakan VBA

salah satu metode iterative untuk mencari akar persamaan adalah metode bisection, penjelasan lengkap tentang apa itu metode bisection dan metode lainya silahkan berkunjung ke sini
http://bloghasnan.blogspot.com/2012/03/metode-iterative-dan-aplikasinya.html

kali ini saya menggunakan module untuk membuat fungsi dalam VBA, sehingga dapat digunakan kapan saja fungsi tersebut dipanggil
membuat module

1. buka MS Excell
2. Masuk ke Developer Tab (ms. 2007),
3. klik Visual basic icon, maka kita akan masuk ke penulisan program
4. insert module, caranya klik kanan, insert, module seperti gambar dibawah berikut

setelah itu anda tinggal menuliskan coding untuk function nya saja

Alogaritma Bisection
kali ini saya menggunakan loop until, penjelasan dan contohnya dapat dilihat disini nie struktur looping

1. baca x0,x1 error
2. loop = 0
3. do
4. loop = loop + 1
5. baca fungsi f(x0), x0
6. baca fungsi f(x1), x1
7. xmid = (xl + xr) / 2
8. fxmid = fx(xmid)
9.  If   (f(xl )* fxmid) > 0 Then
10.   xl = xmid
11.  else
12. x1=xmid
13. end if
14. loop until |fxmid| < error
15. hasil = xmid
16. stop

kurang lebih seperti itu, bila ingin menambahkan minimal iterasi 100 misalnya, maka alogaritma no 14, dapat kita tabahkan menjadi

14. 14. loop until |fxmid| < error atau loop > 100

Source Code
masukkan coding dibawah ini, kedalam module untuk membuat fungsi baru didalam excell


Function bisect(xl, xr, err)
ilps = 0
Do
  ilps = ilps + 1
  fxl = fx(xl)
  fxr = fx(xr)
  xmid = (xl + xr) / 2
  fxmid = fx(xmid)
  If (fxl * fxmid) > 0 Then
     xl = xmid
   Else
     xr = xmid
  End If
  Debug.Print "x=", xmid, "   fx=", fxmid
  Loop Until (Abs(fxmid) < err) Or (ilps > 100)
bisect = xmid
End Function


Function fx(x)
fx = x ^ 2 - 25
End Function

setelah selesai save file anda, secara otomatis anda sudah memasukkan fungsi baru yaitu bisect pada excell yang bisa dipanggil sewaktu-waktu dengan memberikan nilai x1,xr, dan error yang diingikan, tentunya semua tersebut harus dilakukan di cells excel.

Contoh dan Cara memanggil fungsi
sebagai contoh sesuai dengan buku rajaraman : computer oriented numerical control, hal 39, yaitu metode bisectio, diambil fungsi x^2 - d = 0, dengan x0=2, x1=7 dan d = 25

1. funsi tersebut saya tulis pada module

Function fx(x)
fx = x ^ 2 - 25
End Function

2. save file anda
3. kembali ke excell, lalu ketikkan nilai x1,x0, error pada cell yang berbeda
4. panggil fungsi dengan mengetikkan =bisect(x1,x0,error) pada cell yang dituju, lihat gambar berikut bila kurang jelas

hasilnya bisa dilihat pada gmabar dibawah ini

Kesimpulan
dari hasil iterasi didapatkan nilai yang sama yaitu 5.00, besarnya hasil akan sangat tergantung dari nilai error yang dimasukkan, semakin kecil nilai error yang diinginkan maka hasilnya semakin valid, lihat pada gambar diatas.

Read More

Eliminasi gaus Jordan, alogaritma dan pemograman menggunakan VBA

Eliminasi Gaus Jordan sangat bermanfaat untuk proses perhitungan persamaan suku banyak, namun linier, proses perhitungan eliminasi gaus adalah dengan mengeliminasi baris per barisnya sehingga didapatkan matrix berbentuk segitiga, bila proses segitiga selesai, perhitungan variabel bisa dijalankan dengan back subtitusi.

Alogaritma
misalnya diketahui 3 buah persamaan
a11x1+ a12x2 + a13x3 = a14
a21x1+ a22x2 + a23x3 = a24
a31x1+ a32x2 + a33x3 = a34

untuk proses eliminasi x1 dari ketiga persamaan diatas :
1. for i =1 to 3 dan j=1 to 4 read aij
2. end for
3. for i = 2 to 3 in step of 1 hitung
4. u1 = ai1/a11
5. for j = 1 to 4 in steps of 1 do
6. aij = aij-ua1j
7. end for
8. end for

untuk eliminasi x2 dari persamaan ketiga
9. i = 3
10. u = a12/a22
11. for j = 2 to 4 in step of 1 do
12 aij = aij - ua2j
13. end for
14. end for

dari alogarima diatas akan didapatkan matrik segitiga, setelah didapatkan matrik segitia tinggal dilakuakn subtitusi balik, sehingga nilai x1,x2,x3 didapatkan.

Konsep Pemograman
form yang saya pakai saya desain seperti berikut

untuk memulai memasukkan program, double klik tombol hitung, code program yang saya tulis berikut, saya gunakan konsep yang sederhana dan hanya bisa digunakan untuk tiga persamaan dengan tiga konstanta yang tidak diketahui


Private Sub CommandButton1_Click()
Dim a11, a12, a13, a14, a21, a22, a23, a24, a31, a32, a33, a34, hx1, hx2, hx3 As Double
Dim u1, u2, u3 As Double
Dim e21, e22, e23, e24, e31, e32, e33, e34, e342, e332 As Double


a11 = ta11.Text
a12 = ta12.Text
a13 = ta13.Text
a14 = ta14.Text
a21 = ta21.Text
a22 = ta22.Text
a23 = ta23.Text
a24 = ta24.Text
a31 = ta31.Text
a32 = ta32.Text
a33 = ta33.Text
a34 = ta34.Text
' menghitung u
u1 = a21 / a11
u2 = a31 / a11
u3 = a32 / a22
'eliminasi baris 2 dan 3
e21 = a21 - (u1 * a11)
e22 = a22 - (u1 * a12)
e23 = a23 - (u1 * a13)
e24 = a24 - (u1 * a14)
e31 = a31 - (u2 * a11)
e32 = a32 - (u2 * a12)
e33 = a33 - (u2 * a13)
e34 = a34 - (u2 * a14)
' eliminasi baris 2 dan 3, sekaligus menghitung hasil x3, x2, dan x1
e342 = e34 - (u3 * e24)
e332 = e33 - (u3 * e23)
'subtitusi balik
hx3 = e34 / e33
hx2 = ((e24 - (e23 * hx3)) / e22)
hx1 = Val((a14 - (a12 * hx2) - (a13 * hx3)) / a11)
' menulis hasil
thx1.Text = hx1
thx2.Text = hx2
thx3.Text = hx3
End Sub


untuk clear text, silahkan masukkan program seperti berikut,

Private Sub CommandButton2_Click()
ta11.Text = ""
ta12.Text = ""
ta13.Text = ""
ta14.Text = ""
ta21.Text = ""
ta22.Text = ""
ta23.Text = ""
ta24.Text = ""
ta31.Text = ""
ta32.Text = ""
ta33.Text = ""
ta34.Text = ""
thx1.Text = ""
thx2.Text = ""
thx3.Text = ""
End Sub

untuk memudahkan loading form tersebut saya juga memasukkan tombol ke spreadsheet excel, lalu memberikan perintah menampilkan form tersebut seperti dibawah ini

Private Sub CommandButton1_Click()

UserForm1.Show

End Sub

ketika program dijalankan, hasilnya kurang lebih seperti ini

programnya dapat didownload pada embed object berikut, untuk mendownload pastikan browser anda sudah terinstal flash player, butuh waktu untuk melihat tampilan dari box.net
semoga bermanfaat

Read More

Studi Pengaruh Kualitas Grid Terhadap Hasil Simulasi

Tidak semua grid atau mesh yang rapat, kecil-kecil berdampak bagus pada proses simulasi CFD, salah penempatan grid, ujung-ujungnya tambah lama proses iterasi berlangsung, apalagi kalau kita berkeja dengan komputer yang resourcenya terbatas, namun perlu diingat kualitas mesh/grid berpengaruh besar terhadap kualitas dari hasil simulasi CFD, tapi tidak semua tempat membutuhkan kerapatan grid yang kecil.
meshing dengan kualitas bagus dapat meningkatkan akurasi dari hasil simulasi, dan hasil konvergensi saat iterasi berlangsung,

ilustrasi sederhana diatas memperlihatkan perbedaan maksud grid pada kondisi fisik dan grid pada kondisi perhitungan komputer, dalam kondisi fisik, kita dapat mengatur daerah mana yang harus mempunyai grid banyak, rapat dan daerah mana yang renggang, sedangkan pada kondisi perhitungan komputer, grid tersebut dihitung berdasar kan jumlah i dan j nya, jadi semakin banyak jumlah cell tentunya semakin besar beban kerja komputer. oleh karena itu dengan pemahaman fisika yang benar, kita dapat memperkirakan daerah mana yang terjadi perubahan besar, misalnya contact surface, daerah belokan dsb, sedangkan daerah luar dimana diperkirakan perubahan tidak terjadi significant, besar gridnya dapat dibuat lebih besar dan jarang, namun perlu diingat perpindahan perubahan grid harus smooth, agar proses perhitungan dapat konvergen dan tidak terjadi error

gambar diatas memperlihatkan struktur grid yang berbeda di tiap titiknya,  pada daerah yang diperkirakan terjadi perubahan aliran, terutama daerah kontak, free surface dibuat grid yang kecil dan rapat, sehingga setiap perubahan yang terjadi di daerah itu dapat divisualisasikan dengan baik.

Jenis Mesh
secara garis besar dibagi menjadi dua bagian, 2D dan 3D
untuk 2D yang paling sering digunakan adalah quad dan triangle, beberapa jenis mesh yang digunakan dapat dilihat pada gambar berikut

Mesh Design Guidelines
berikut beberapa aturan yang harus diperhatikan untuk mendapatkan hasil simulasi CFD yang bagus
1. dekat dengan boundary layer, kontak layer, gunakan grid yang rapat, misalnya pada contoh di bawah ini

2. Check apakah jumlah grid berpengaruh besar terhadap hasil simulasi, bila ya, gunakan jumlah grid yang lebih kecil, agar perubahan kecil pun dapat terdeteksi, bila jumlah grid tidak berpengaruh besar terhadap hasil simulasi, berarti jumlah grid sudah sesuai.
3. perubahan cell dari yang rapat/kecil ke cell yang besar, diusahakan smooth, kalau perubahan mesh terlalu besar, hal ini akan menyebabkan proses iterasi berlangsung lama, dan hasilnya simulasi kurang bagus.
4. hindari mesh yang membentuk skew, atau tipis panjang dan kurang teratur, misalnya segi empat namun satu sudutnya di dalam, karena hal ini akan menyebabkan error pada proses iterasi, selain itu waktu yang dibutuhkan juga semakin lama.

Read More

Integrasi numerik antara metode simson dan trapezodial

dalam posting kali ini saya akan emncoba mejelaskan secara teoritis mengenai metode simson dan trapezodial, berdasarkan beberapa referensi, evaluasi nilai integral yang sudah sering kita pakai adalah metode kalkulus, metode ini disebut dengan metode exact, namun evaluasi dengan metode kalkulus tidak akan berhasil pada fungsi dengan bentuk yang kompleks, misalnya F(x) = 2x^sin 2x^3x, metode yang lebih sederhana (walau lebih komplek kalau dimengerti, tapi sederhana bagi komputer) adalah dengan metode numerik, dua metode yang dibahas dalam posting ini adalah metode simson dan trapezodial
Metode Simson
perbandingan pemrograman, alogaritma dan contohnya dapat dilihat di
http://bloghasnan.blogspot.com/2012/03/perbandingan-hasil-integrasi-numerik.html
secara sederhana, metode ini dapat dilihat pada gambar dibawah, untuk fungsi sinx,

 

 metode simpson dapat ditulis dengan

 yang artinya fungsi f ditabulasikan pada point x0, x1 dan x2 dengan spasi jarak yang sama, jarak ini disebut dengan h.
karena fungsi yang dipakai adalah pendekatan mengunakan quadratic polynomial, aturan simson akan menghasilkan nilai exact ketika pendekatan integralnya sampai derajat kubik.


 sebagai contoh pada fungsi sin x (kurva warna hitam) diatas pada interval [0, phi/2]  sehingga f(x=0) = 0, bila dihitung dengan simson rule


Metode Trapezodial
 metode ini menggunakan konsep menghitung luasan dengan cara menghitung luasan antara x1, dan x2 terhadap fungsi fx, dari gambar dibawah berikut dapat kita lihat semakin kecil h, maka nilai yang didapatkan akan semakin mendekati exact

sebagai perbandingan dengan metode simson, gambar dibawah ini adalah simulasi hasil perhitungan untuk sin x menggunakan metode trapezodial
 
dapat kita lihat pada gambar diatas, untuk fungsi yang sama, nilai dari simson lebih mendekati exact jika dibandingkan dengan trapezodial, tapi menurut saya selama h nya sekecil mungkin, maka nilai dari trapezodial pun akan semakin mendekati exact.

Read More

Perbandingan Hasil Integrasi Numerik menggunakan Simson dan Trapezodial

Secara teoritis memang metode simson akan menghasilkan hasil yang lebih akurat dibandingkan dengan Trapezodial, langkah termudah membuktikannya adalah dengan membuat program untuk keduanya lalu membandingkannya. sesuai dengan buku [1] hal 148, contoh 8.3 dari table yang ada, saya membuat program untuk menghitung secara dua metode diatas, form yang saya buat adalah seperti gambar berikut ini

 

Metode Simson

untuk simson, parameter yang dimasukkan dalam perhitungan adalah nilai x terendah atau x1, nilai h, dan jumlah data (n). nilai integral metode simson dihitung dengan 

  

 

Alogaritma

alogaritma yang digunakan adalah

1. baca n,x1,h

2. for i = 1 to n+1

3. baris n = x1

4. x1 = x1 + h '(menuliskan nilai x pada kolom)

6. next 1

7. Hitung S = h/3 * (f1+4*f2+2*f3+4*f4+2*f5+4*f6+...+fn+1)

8. tulis S

9. stop

Pembuatan Program
buka excel baru, pastikan toolbar developer sudah terpasang, klik design mode, lalu masukkan command button 2 buah, 1 buah untuk simson, 1 buah untuk trapezodial
nilai f(x) karena sudah ditentukan tulis mulai dari B2 sampai B11, sedangkan nilai x karena mempunyai nilai yang berurutan dengan interval tertentu dapat ditulis dengan program.
double klik command button 1, lalu tulis programnya sebagai berikut

Private Sub CommandButton1_Click()
Dim n, S, jum As Double
Dim h, xi As Single

n = Cells(2, 5)
x1 = Cells(3, 5)
h = Cells(4, 5)
For i = 1 To n + 1
    Cells(i + 1, 1) = x1
    x1 = x1 + h
Next i
     S = (h / 3) * (Cells(2, 2) + 4 * Cells(3, 2) + 2 * Cells(4, 2) + 4 * Cells(5, 2) + 2 * Cells(6, 2) + 4 * Cells(7, 2) + 2 * Cells(8, 2) + 4 * Cells(9, 2) + 2 * Cells(10, 2) + 4 * Cells(11, 2))
    Cells(6, 5) = S
   
End Sub

 Metode Trapezodial
 untuk metode trapezodial, hanya nilai n dan h yang perlu dimasukkan, jumlah n dan h saja, untuk mempermudah perbandingan, nilai n dan h yang dimasukkan bernilai sama dengan simson, begitu juga dengan data yang akan dibaca, karena itu tidak perlu menuliskan f(x) dan x lagi.
nilai integral trapezodial dihitung dengan

 

Alogaritma

secara alogaritma metode trapezodial lebih sederhana, untuk kasus ini, saya menggabungkan nilai f2 hingga fn-1 untuk mempermudah perhitungan

1. baca n,h

2. For i = 1 To n - 1
3.  a = a + baris kedua hingga baris n-1
4. Next i
5. Hitung   S = h * ((Cells(2, 2) / 2) + a + (Cells(n + 2, 2) / 2))
6. Tulis S

7. Stop

Pembuatan Program

masih pada spreadsheet yang sama dengan simson, double klik command button 2, lalu tulis program seperti berikut

Private Sub CommandButton2_Click()
Dim h, n, S, a As Single
n = Cells(2, 8)
h = Cells(3, 8)
For i = 1 To n - 1
   a = a + Cells(2 + i, 2)
Next i
    Cells(7, 7) = a '
    S = h * ((Cells(2, 2) / 2) + a + (Cells(n + 2, 2) / 2))
    Cells(6, 8) = S
End Sub

hasilnya dapat dilihat pada gambar dibawah berikut

 

dapat dilihat nilainya berbeda,  dibuku nilai akhirnya adalah 3,1 untuk simson, perbedaan dengan di buku karena di buku 2 nilai f(x) awal dihitung dengan trapezodial terlebih dahulu. sedangkan nilai perhitungan trapezodial sudah sama persis dibuku yaitu 3.1

filenya silahkan di download pada embed object berikut, semoga bermanfaat

Read More

Metode Iterative dan aplikasinya

metode ini dapat dipahami sebagi salah satu metode matematika untuk menyelesaikan persamaan atau kumpulan persamaan, dengan cara memasukkan nilai tebakan awal, lalu dilakukan pendekatan sampai nilai tersebut konvergen, pendekatan tersebut dilakukan sampai nilai error sesuai atau lebih kecil dari yang kita inginkan, karena komputer saat ini sudah berkecepatan tinggi, memasukkan nilai error sampai 0.00001 pun tidak akan menjadi kesulitan.  kondisi error lebih kecil dari pada yang kita inginkan disebut konvergen.

misalnya pada permasalahan mencari akar persamaan, perhitungan secara exact dapat dilakukan dengan memakai metode eliminasi gaus, misalnya pada Ax+b=0, namun pada persamaan non linier, metode iterative sangat banyak digunakan, karena persamaan, suku pangkat sangat susah untuk diselesaikan secara exact.
ada beberapa metode iterative yang biasa dipakai antara lain :
1. Metode newton raphson
2. Metode Secant
3. Metode Bisection
4. Metode False Position
sebenarnya masih banyak metode lain yang lebih rumit dan memusingkan, saya sebut metode advance, misalnya :
1. Newton Krylov
2. Arnoldi Iteration
3. Jacobi Method

penjelasan singkatnya adalah sebagai berikut
1. Metode Newton Raphson
saya sudah mencoba membuat alogaritma dan pemogramannya menjadi sebuah fungsi di visual basic, silahkan check di  http://bloghasnan.blogspot.com/2012/03/pemograman-newton-rapshon-sebagai.html,  kelemahan dari program yang saya buat tersebut adalah, harus memasukkan fungsi secara manual, sehingga bila terdapat fungsi lain, kita harus menuliskannya dahulu ke syntax code. metode ini ditemukan oleh Isaac Newton dan Joseph Raphson, metode ini dapat mencari nilai pendekatan dari akar persamaan sama dengan nol.
newton raphson untuk satu fariable dapat dijelaskan sebagai berikut

 misalnya diketahui sebuah fungsi f(x)=0 (garis biru), tebakan pertama (x1) menghasilkan slope (garis merah), pada titik perpotongan dengan sumbu maka didapatkan nilai x2 yang lebih mendekati, nilai x2 didapatkan dari nilai x1 dikurangi f(x)/f'(x), dari nilai x2 dihitung nilai f(x) lalu didapatkan slope yang lebih mendekati, dan seterusnya sampai pendekatan tersebut mendekati nol, seberapa dekat?? semampu komputer menghitung saya rasa.
Definisi dari turunan f'(x) sebuah fungsi f(x) adalah

sehingga nilai xn adalah

2. Metode Secant
metode ini dikembangkan terpisah dari newton, namun secara prinsip metode secant adalah metode untuk menentukan akar-akar persamaan yang sering disebut sebagai pendekatan finite different dari metode newton-raphson, untuk lebih jelasnya perhatikan gambar berikut ini

sesuai pada gambar diatas, untuk menebak nilai yang mendekati f(x) maka dibutuhkan dua buah tebakan, yaitu x0 dan x1, lalu didapatkan nilai x2, rumus untuk menghitung nilai x ke n untuk metode secant adalah

3. Metode Bisection
metode ini adalah metode pencarian akar persamaan dengan cara membelah suatu fungsi dalam interval tertentu, lalu interval tersebut diperkecil, secara berurutan sampai didapatkan nilai x yang mendekati f(x)=0, secara grafis dapat dilihat pada gambar dibawah berikut

analisis intervalnya

alogaritmanya adalah :

INPUT: Function f, endpoint values a, b, tolerance TOL, maximum iterations NMAX
CONDITIONS: a < b, either f(a) < 0 and f(b) > 0 or f(a) > 0 and f(b) < 0
OUTPUT: value which differs from a root of f(x)=0 by less than TOL

N ← 1
While N ≤ NMAX { limit iterations to prevent infinite loop
  c ← (a + b)/2 new midpoint
  If (f(c) = 0 or (b – a)/2 < TOL then { solution found
    Output(c)
    Stop
  }
  N ← N + 1 increment step counter
  If sign(f(c)) = sign(f(a)) then a ← c else b ← c new interval
}
Output("Method failed.") max number of steps exceeded

(Burden, Richard L.; Faires, J. Douglas (1985), "2.1 The Bisection Algorithm", Numerical Analysis (3rd ed.), PWS Publishers)

4. False Position
 metode ini sering disebut juga dengan regula falsi yaitu metode untuk mencari akar persamaan dengan cara menebak x lalu fungsi akan mengembalikan dengan arah berlawanan, proses tersebut diulang sampai didapatkan nilai f(x) dengan error mendekati nol

bila diambil dari dua titik, didapatkan

dengan y=0, dan y1=f(x1) penyelesaian Xn dapat didekati dengan iterasi

metode manakah yang lebih effisien, lebih cepat melakukan perhitungan? sepertinya perlu dibuat programnya satu per satu lalu dibandingkan hasilnya, ada yang mau bantu?


Referensi
1. iterative for optimization : www.caam.rice.edu/~zhang/caam554/KelleyBooks/fr18_book.pdf
2. Iterative for linier and non linier system : www.caam.rice.edu/~zhang/caam454/KelleyBooks/fr16_book.pdf
3.   Iterative Solution Methods :  Oleh Owe Axelsson
4. Solving nonlinear equations with Newton's method  Oleh C. T. Kelle
5. Numerical analysis oleh Richard L. Burden, J. Douglas Faires
6.  Computer solution of large linear systems  Oleh Gérard Meurant

Aknowledment
Many thanks to Google books.

Read More