Data Radiasi Wilayah Jakarta tahun 2011

data radiasi terbaru berikut sangat cocok untuk proses perhitungan berikutnya, ada tiga data radiasi yang akan saya bandingkan, yaitu
1. hasil pengukuran langsung oleh Ir. Sudjito Ph.D (guru baik saya waktu kuliah S1, salam hormat untuk beliau) namun data yang dapat dikumpulkan adalah dari tahun 1970 sampai dengan 1992, data terbaru saya belum menemukan
2. data hasil simulasi dari Dr. Susandi (ahli meteorology dari ITB), datanya untuk tahun 2010
3. Data paling akhir adalah dari Institute Agricultural technology Tokyo, data untuk tahun 2011, datanya tersedia untuk 12 bulan, seperti pada tampilan gambar dibawah ini

untuk data radiasi lainya, saya masih mentabulasi, berikut hubungan data tersebut dengan keperluan penelitian yang akan dikerjakan.
menanggapi pertanyaan Dr. Indra kemarin, bagaimana membuat model untuk radiasi dan pengaruhnya terhadap dinding kamar yang terpapar langsung dengan sinar matahari, saya baru mendapat beberapa jurnal saja, sehingga rasanya belum pantas untuk ditulis. pada posting selanjutnya saya akan mencoba untuk menulis hubungan dan bentuk modelnya

Read More

Memahami sifat-sifat dasar aliran diantara dua plat datar

ada tiga hal yang akan dibahas dalam posting kali ini untuk memahami sifat-sifat dasar aliran
1. lapisan batas
2. free surface flow (tsunami)
3. aliran diantara 2 plat datar
sebelum jauh memahami konsep tiga aliran diatas, perlu dipahami dasar pemikiran untuk memahami aliran fluida yaitu kerapatan (density), berat jenis (specific gravity), tekanan (pressure), kekentalan (viscosity).

1. lapisan batas
penentuan lapisan batas pada fluida atau boundary condition sangat berpengaruh terhadap apa yang akan kita teliti, dan apa yang akan kita bahas.
sering kali kita salah mengenai aliran viskos, ada saut hal yang penting untuk diketahui bahwa lapisan batas sangat perlu diperhatikan, misalnya jika bilangan reynold cukup besar, efek viskos penting hanya di bagian lapisan batas di dekat benda, lapisan batas diperlukan fluida untuk menempel tanpa kondisi slip, sehingga fluida dapat mengalir, diluar lapisan batas peruabhan kecepatan tegak lurus terhadap aliran relatif kecil.

 2. Lapisan batas pada sebuah plat datar
terdapat banyak jenis lapisan batas yang dapat diperhitungkan dalam aliran, situasi yang paling sederhana misalnya adalah lapisan batas pada sebauh plat datar dengan panjang tidak terhingga, di atasnya mengalir sebuah fluida viskos, tak mampu mampat seperti gambar diatas, tentunya lapisan batas tersebut akan berbeda jika bentuk benda berbeda, misalnya untuk benda seperti airfoil, silinder dsb.
kita anggap bilangan reynold cukup besar nilainya, sehingga hanya fluida yang ada diatasnya yang merasakan effect plat tersebut, untuk kasus ini karena panjang tidak terhingga tidak bisa menghitung bilangan reynold. sehingga Reynold dapat didekati dengan Rex = Ux/v, yaitu bilangan reynold akan berubah menurut kecepatan pada daerah x.

dengan tebal plat dapat ditulis dengan

3.aliran pada dua plat datar
pada jenis aliran ini pada prinsipnya sama dengan aliran terbuka, namun dikarenakan boundary layernya ada dua, misalnya dengan pendekatan 2D, maka bentuk alirannya berupa parabolik

rumus yang dipakai untuk menghitung adalah

total linier flow dapat dihitung dengan proses integrasi

pembahasan tentang aliran pada dua plat datar, juga sudah saya berikan di posting sebelumnya. untuk penurunan rumus lebih lengkap silahkan check website di bawah berikut
http://www.ecourses.ou.edu/cgi-bin/ebook.cgi?doc=&topic=fl&chap_sec=08.1&page=theory

Refferensi
1. Boundary-Layer Theory  Oleh Hermann Schlichting,K. Gersten
2. dasar-dasar fenomena transport oleh james

Read More

moody diagram dan viskositas : cara penggunaan

Ya Moody diagram sangat bermanfaat untuk menghitung aliran yang terjadi pada suatu pipa, sejujurnya saja sangat susah untuk menghitung nilai friction didalam pipa, apalagi bila pipa tersebut mempunyai panjang yang lumayan, sehingga perbandingan antara diameter dan panjang pipa sangatlah kecil.
cara yang paling mudah adalah dengan pembacaan melalui moody diagram, tanpa mengetahui dengan pasti nilai dari kekasaran pipa, kita dapat memperkirakan dengan mudah melalui pembacaan diagram ini.

Dasar teori

head loss pada pipa karena gesekan dapat dihitung dengan persamaan Darcy-Weisbach seperti dibawah ini

dengan,  h = head loss
             f = friction factor
             L = length of pipe
             v = velocity of fluid trough pipe
             D = Diameter of pipe
             g = acceleration due to gravity
Diagram Moody memberikan faktor gesekan pipa. Faktor ini dapat ditentukan oleh bilangan Reynold dan kekasaran relatif dari Pipa.
bila pipa semakin kasar, maka kemungkinan turbulent akan semakin besar, kekasaran relatif didefinisikan sebagai

dengan,
 e = absolute roughness
D = diameter of pipe

sedangkan bilangan reynold didefinisikan sebagai

dengan,
R = Reynolds number
D = diameter
v = velocity
ζ = kenimatic viscosity of fluid

ok. moody diagram dapat dilihat pada diagram dibawah berikut

Cara Baca

 Dengan melihat diagram Moody itu menunjukkan bahwa sudut kanan atas benar-benar turbulent dan bagian atas kiri adalah laminar.
Untuk menentukan faktor gesekan,  nilai kekasaran relatif dari pipa dapat dilihat di sebelah kanan. Kemudian cari  Reynolds number di bagian bawah, tarik keatas sampai memotong, sebelah kiri akan didapatkan nilai faktor gesekan. dan jenis aliran apakah turbulen ataukah laminer

Contoh Pemakaian

selamat belajar

Read More

aliran dengan perbesaran mendadak

saya menemukan video bagus untuk memahami proses aliran pada pembesaran mendadak, silahkan check dibawah ini, untuk pembahasan dan dasar teorinya, mohon tunggu ya

Read More

Pegambilan Data untuk Solar Water Heater Project (tugas besar)

Data- data berikut diambil pada hari minggu, namun pada hari tersebut terjadi hujan mulai dari jam 10.00 sampai dengan jam 15.00, hal ini menyebabkan suhu yang diambil lebih rendah dari yang diinginkan

Pengukuran suhu sekitar rumah 
Jam       Suhu (celcius)
05.00    27.7
06.00    28.5
07.00    29.2
08.00    29
09.00    29.3
10.00    28.3
11.00   28.7
12.00   29.3
13.00   29.4
14.00   28.8
15.00   28.5
16.00   28.5
17.00   28.5
18.00   28.4

Posisi Bumi  
LS 6° 22' 21 BT 106° 49' 39
Ketinggian tempat 
Hasil pengukuran barometer adalah 170 m, namun barometer yang saya pakai belum dikaliberasi, perkiraan setelah di kaliberasi adalah 120 M

Kebutuhan Air
untuk mesin cuci adalah 8 hingga 10 liter untuk rendaman pertama kali saja, tergantung dari jumlah pakain yang akan dicuci, suhu yang dipakai 70-80 C.
untuk mandi 6 liter dengan suhu 55 C hingga 60 C

Data radiasi

dalam bentuk tabel

Sumber :
 Meita Rumbayan,    Asifujiang Abudureyimu,  Ken Nagasaka,[2012] Mapping of solar energy potential in Indonesia using artificial neural network and geographical information system.  Tokyo University of Agriculture and Technology, Tokyo, Japan

Read More

Memahami Viskositas suatu Fluida

Pengertian Viskositas

Viskositas diartikan sebagai tahanan internal terhadap aliran, dan beberapa ahli dapat juga mendefiniskan sebagai gesekan dari fluida.
Viskositas adalah nilai yang diukur dari tahanan fluida yang berubah bentuk karena tegangan geser (shear stress) maupun tegangan tarik (tensile stess). Dalam kehidupan sehari-hari dapat kita jumpai pada fluida seperti air, jelly, madu, susu, dapat pula dikatakan karena tegangan geser air kecil, sehingga mudah jatuh maka viskositas air lebih kecil dibandingkan dengan madu, karena madu mempunyai tegangan geser internal yang lebih besar, sehingga saat diteteskan madu lebih sulit untuk jatuh dibandingkan dengan air. Pengertian yang paling sederhana semakin kecil nilai viskositas maka semakin mudah suatu fluida untuk bergerak.
Fluida ideal adalah fluida yang tidak memiliki tahanan gesekan terhadap tegangan geser biasanya disebut juga dengan inviscid fluid, sedangkan fluida normal selalu mempunyai tahanan gesekan terhadapa tegangan geser, yang disebut dengan viskos fluid.
Rheology adalah ilmu yang mempelajari aliran suatu benda. Yang didalamnya terdapat juga konsep viskositas, thermofluid dan hubungan lainnya.

Tegangan geser dan viskositas

hubungan antara tegangan geser dan viskositas dan perubahan kecepatan dapat dipahami pada kasus aliran diantara dua plat datar, misalkan jarak antar palt adalah y, dan diantara plat tersebut terdapat fluida dengan isi yang homogen, asumsikan bahwa plat sangat luas, dengan luas A yang besar, pengaruh rusuk dapat dianggap tidak ada. pada plat bagian bawah diaanggap tetap lalu diberikan gaya sebesar F pada plat atas. bila ternyata gaya ini menyebabkan material diantara dua plat bergerak dengan perubahan kecepatan u. gaya yang diberikan proposional dengan luas dan perubahan kecepatan

gaya yang bekerja dapat ditulis dengan

Sehingga tegangan geser dapat ditulis dengan

sehingga untuk aliran laminar, teganan geser dapat dinyatakan sebagai

Atau dapat kita ambil poitnya sebagai berikut
-    Tegangan geser berbanding lurus dengan perubahan kecepatan dengan arah tegak lurus layer.
-    Teganan geser juga berbanding lurus dengan nilai viskositas suatu fluida, semakin besar nilai viskositas fluida, semakin besar pula tegangan geser yang dibutuhkan untuk mengalirkan fluida.

Tipe Viskositas

Newtonian: fluida yang memiliki viskositas konstan, misalnya air dan kebanyakan gas mempunyai viskositas yang konstan.
• Shear thickening: viskositas akan naik dengan kenaikan laju geseran.
• Shear thinning: viskostias menurun dengan pertambahan geseran,
• Thixotropic: material yang mempunyai viskositas rendah ketika di gerakkan, diberikan tegangan
• Rheopectic: materials yang mempunyai viskositas meningkat ketika digerakkan, terkena benturan, maupun diberi tegangan. .
• A Bingham plastic  adalah material yang mempunyai wujud solid ketika teganan kecil tetapi mengalir ketika diberi tegangan besar is a material that behaves as a solid at low stresses but flows as a viscous fluid at high
stresses.

Read More

langkah per langkah simulasi aliran perbesaran mendadak

aliran dengan perbesaran mendadak mempunyai karateristik tersendiri, terutama pada bagian kosongnya, nah.. untuk lebih jelasnya silahkan ikuti langkah berikut ini
buka CFDSOFT anda, tentunya harus tersambung dengan koneksi UI, lalu klik file input, atau pada command promp, ketikkan in = input

 

langkah selanjutnya adalah mengatur domain dimensi yang akan digunakan, dalam latihan ini digunakan panjang 10 m dan tinggi 2 m, jumlah cell yang dipakai adalah 100 untuk arah i dan 20 untuk arah j

 

tampilan dari grid yang dipakai adalah sebagai berikut, langkah selanjutnya adalah mengatur jenis grid yang dipakai, atur sedemikian rupa sehingga ukuran yang didesain sesuai untuk aliran perbesaran mendadak, misalnya utuk dua buah pipa dengan diamater berbeda. atur wall 1(warna hijau) dan inlet (warna biru)

kemudian atur wall tersebut, atur input berupa tekanan statik pada input sebelah kanan, sedangkan pada sebelah kiri berikan tekanan statik = 0

 

selanjutnya adalah pengaturan konstantan fiskal,  konstanta yang diatur adalah

- densitas

- viskositas

setelah pengaturan selesai, lakukan iterasi 2000 kali iterasi, hasilnya seperti dibawah berikut

Hasil Simulasi Aliran Perbesaran Mendadak

total tekanan, hasil simulasi menunjukkan terjadi penurunan tekanan yang cukup significant setelah melewati luas dengan penampang lebih besar, hal ini disebabkan karena dengan permukaan yang luas aliran dapat bergerak mengisi volume yang kosong, karena volume ruang lebih besar, tekanan yang terjadi menjadi mengecil, sesuai dengan rumus gas ideal bahwa tekanan berbanding terbalik dengan volume.

kecepatan, begitu juga dengan kecepatan, besarnya kecepatan langsung turun begitu melewati saluran yang lebih besar, tentunya hal ini karena pengaruh hukum kekekalan massa dan momentum, yang patut dilihat adalah adanya aliran dissipative effect karena shock wave.

perhatikan gambar dibawah berikut, adanya aliran balik yang berputar tepat setelah luasan/ volume pada pipa berubah merupakan sifat dari fluida, saat suatu fluida menerima perubahan arah aliran secara mendadak, maka aliran yang semula laminer akan berubah menjadi turbulent, sifat ini juga memperkuat posting sebelumnya tentang fully developt region, bahwa aliran butuh jarak tertentu untuk mencapai daerah tersebut, adanya perbesaran mendadak tersebut menjadikan aliran menerima perubahan mendadak yang menyebabkan arah aliran tidak terkendali.

Bagaimana dengan perubahan secara beraturan ??

dengan cara yang sama diatas, kita mensimulasikan perubahan aliran dengan bentuk yang lebih landai, hasilnya sebagai berikut

tekanan,
dapat kita lihat perubahan tekanan secara kasat mata, sama dengan pada aliran perbesaran mendadak, namun, shockwave effect tidak dapat kita temukan disini.

kecepatan,
shock wave effect yang menyebabkan aliran balik dan turbulent pada daerah didekat perubahan sudah tidak nampak, semakin smooth perubahan maka gejolak shock wave tidak akan terlihat, hal ini bermanfaat pada aliran pipa, terutama sambungannya, bila sambungan pipa terjadi perbesaran mendadak, kemungkinan besar terjadi shock wave, dan menyebabkan sebagian aliran berputar balik, turbulent, akibat buruknya, bila kecepatan lumanyan besar, cavitasi bisa aja terjadi.

Refferensi
1. Dasar-2 Fenomena Transport/1
2. Hidraul : Suatu Penyeselaian  Oleh Amer Nordin Darus

Read More

Flow chart untuk menghitung solar water heater

langkah-langkah secara detail untuk melalakukan perhitungan water heater adalah sebagai berikut :

1. pemasukan data radiasi, perhitungan hari, nilai indeks awan (KT) suhu air masuk, posisi lintang dan bujur.

2. setelah data lengkap dilakukan perhitungan declination yaitu posisi matahari terhadap daerah tertentu, solar hour angle, yaitu posisi setiap jam matahari dan suhu udara di langit

3. selanjutnya dengan memasukkan tambahan suhu air panas yang diingikan dan jumlah air yang dibutuhkan dihitung beban pemanasan

4. memilih jenis collector

5. menghitung nilai Q berdasarkan jenis collector

6. menambahkan nilai effisiensi dan heat lose akibat sakuran pipa, kita akan mendapatkan luas collector yang dibutuhkan
selengkapnya seperti dibawah berikut

Read More

transient analysis : contoh pada proses pendinginan mold

bila pada posting sebelumnya, banyak membahas mengenai masalah yang diselesaikan melalui CFD secara steady state, dalam posting kali ini kita akan membahas untuk proses fluida maupaun termal yang terikat waktu, atau dalam bahasa ilmiahnya disebut transient analisys.
contoh
contoh sederhana pemakaian metode ini adalah misalnya logam yang dipanaskan lalu dibiarkan begitu saja di ruangan terbuka, butuh waktu berapa lamakah sampai suhu logam tersebut sama dengan lingkungan? penyelesaian permasalahan tersebut adalah menggunakan metode transient analysis.
lebih luas lagi segala permasalahan engineering yang melibatkan waktu baik untuk proses thermal dan fluida dapat diselesaikan secara transient, silahkan coba googling banyak sekali permasalahan yang dapat diselesaikan dengan metode ini, mulai dari hal sederhana seperti pemanasan air secara alami oleh matahari sampai dengan proses pendinginan reaktor nuklir.
Injection Mould
berhubung dari 6 tahun lalu hingga sekarang saya berkecimpung dalam industi Injection Mould, ternyata proses analisa injeksi mold terutama proses perpindahan panas yang digunakan dapat diselesaikan dengan transient analysis, pada proses pendinginan mold, terjadi proses perpindahan panas dari material plastik yang di injeksikan kedalam cavity bersuhu sekitar 230 C, lalu didinginkan secara cepat melalui saluran cooling pada mold dengan suhu 25-80 C, hasilnya produk dikeluarkan pada suhu sekitar 40-60 C, lalu didinginkan perlahan di udara terbuka sampai suhu ruangan.
proses konduksi yang terjadi pada mould dapat ditulis dengan [1]

 dengan nilai alfa adalah

alfa adalah thermal diffusivity, setiap jenis material plastik mempunyai thermal diffusivity yang berbeda beda
sedangkan nilai dari alfa adalah rasio thermal konduktivitas (K) dengan densitas dan Spesific Heat (Cp)

Thermal diffusivity
bila spesific heat digunakan untuk mengukur energy, thermal diffusivity adalah ukuran laju energi yang dikeluarkan oleh plastik, thermal diffusivity ini akan berubah menurut waktu, untuk logam nilai thermal diffusivity lebih dari 100 kali lipat nilai plastik. meskipun thermal diffusivity terpengaruh pada thermal konduktivitas, spesific heat pada tekanan konstan dan densitas yang berubah menurut suhu, namun nilai thermal diffusivity untuk plastik relatif konstan.[2]

semoga dapat menambah wawasan kita semua

refferensi
[1] Plastics Manufacturing Systems Engineering  By David O. Kazmer
[2] Plastic Product Material and Process Selection Handbook  Oleh Dominick V. Rosato,Donald V. Rosato,Matthew V. Rosato

Read More

Mengasah Intuisi Engineering

terdapat dua hal yang wajib diperhatikan untuk mengasah intuisi seorang engineer atau perekayasa
1. insight, berpikir secara insight wajib diperlukan bagi semua engineer, sehingga setiap masalah yang menuntut penyelesaian, dapat diselesaikan langsung ke akar permasalahan, insight atau berpikir secara mendalam, dapat dilatih dengan membuka wawasan akan fenomena alam yang terjadi di lingkungan sekitar, misalnya pada kasus aliran fluida dalam ruang dan sekaligus hubunganya dengan kenyamanan. kenapa di malam hari suhu kamar saya masih terasa panas? dari satu pertanyaan tersebut harus diurai sebanyak mungkin kemungkinan penyebab fenomena tersebut, dimulai dari pengaruh luar, apakah sumber panas diluar? matahari misalnya, apa saja yang terjadi dan patut diperhitungkan oleh matahari
- sudut datang
- posisi ketinggian tempat
- letak bujur dan lintang
- posisi sinar matahari
- radiasi matahari
- suhu luar ruangan
- perubahan suhu per jam, mauapun per hari
- suhu tanah
pengaruh tembok, yang patut diperhitungkan
- tebal tembok
- letak tembok terhadap penyinaran matahari
- jenis material tembok
- koeffisien konduksi, konveksi dan radiasi
- suhu di dalam dan di luar tembok
selanjutnya masuk kedalam ruangan, untuk melihat faktor apa saja yang berpengaruh
- jumlah manusia
- peralatan yang dihidupkan yang mengakibatkan sumber panas, lampu, setrika, TV
- volume ruangan
- jarak lantai dengan atap
- posisi jendela, ventilasi, pintu
- luas ventilasi
bagaimana dengan efek yang mempengaruhi orang merasa nyaman dalam ruangan
- suhu?
- kelembapan?
- aliran udara?
- kecepatan udara ?
- jumlah udara, atau masa udara yang mengalir?
- atau memang semua bepengaruh?
setelah semua faktor digali lebih jauh, langkah selanjutnya adalah memilah faktor yang mempunyai hubungan penting dan berpengaruh lebih banyak dibandingkan dengan faktor lain, dengan memasang konstrain, satu per satu pengaruh tersebut akan diketahui karateristiknya,  yang selanjutnya bisa disusun dalam suatu kesimpulan
2. forsight, berpikir jauh untuk kemajuan kedepan, jadi misalnya untuk kasus diatas, apa yang harus kita lakukan agar orang merasa nyaman dalam ruangan untuk beberapa dekade ke depan? memakai AC kah? berapa PK yang sesuai, dimana letaknya yang paling efektif? memakai natural ventilation? bagaimana cara kerjanya? bagaimana pengaturannya?
dari berbagai pertanyaan dan pemikiran jauh untuk kemajuan selanjutnya, munculah ide-ide engineering untuk membuat orang merasa nyaman dalam ruangan.
saya secara pribadi cenderung pada natural ventilation, karena ramah lingkungan, hemat listrik,  dan sejuknya alami, bagaimana dengan anda?

Read More

Pemodelan Aliran Laminer pada Dua Plat Datar

nah, berikut ini adalah penurunan rumus untuk aliran laminer pada dua plat datar, langkah per langkah penurunan rumus dapat dilihat pada slide dibawah ini,  intinya, perubahan gradient tekanan arah x adalah sesuai dengan viskositas aliran dibagi dengan kuadrat tinggi aliran

Read More

Menentukan koefisien perpindahan panas konveksi : UTS 4

Tentukan , secara numerik, koefisien perpindahan panas konveksi untuk soal no. 3. Bandingkan dengan hasil analitis. Jelaskan jawaban saudara

untuk menghitung koeffisien konveksi thermal, dapat dilakukan dengan persamaan Nusselt number, Nu adalah fungsi dari gradient suhu terhadap x,

 

h = koefisien konfeksi

k = konduktivitas termal
d = tinggi aliran
T = temperatur
x = jarak x

dengan integrasi suhu terhadap jarak x, akan didapatkan Nusselt number, maka nilai koeffisien konveksi dapat dicari dengan (Nu.K)/d.

Proses pengambilan data sudah dijelaskan pada nomer 1 dan nomer 3 diatas, 

sebagai contoh saya ingin mengetahui koefisien perpindahan panas pada titik ke 6, data yang dipakai seperti dibawah tampilan di bawah berikut, silahkan langsung download, tampilan preview kadang error karena mengandung active x VBA

atau, kurang lebih data yang dipakai sebagai contoh adalah

setelah melakukan proses regresi polynomial, dan menghitung koeffisien didapatkan nilai dari fungsi termperatur sebagai berikut
T=Y = 0.1158X^2-5.2199X+332.4
dT / dx = 0.232 (x)  –5.2199
Persamaan Q konduksi fluida = Q konveksi
k A dT/dx = h A dT
h L /k = dT/dx
h = k (dT/dx) /L
dan k =0.0241, maka nilai h adalah, dengan jarak x =0.06 dan L = 1
h = (0.0241)*(0.0232*(0.06)-5.2199))/1

h = 0.125464626 kJ/K m^2

untuk mencari koeffisien dititik lain, dapat dilakukan dengan mengganti nilai x

Read More

Pengaruh Flux Panas pada plat dan aliran fluida : UTS 3

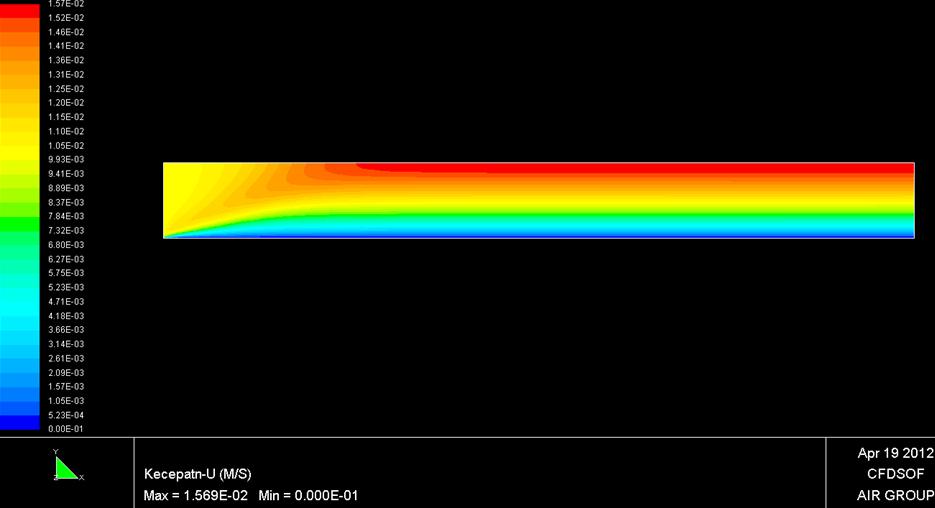
Jika bagian bawah pelat (soal no 1) diberikan fluks panas, tentukan, secara numerik, fungsi profil temperatur pada lapisan batas termal. Bandingkan dengan hasil analitis. Jelaskan jawaban saudara

Dari hasil simulai penambahan flux panas dapat dilihat mampu merubah distribusi temperature dan kecepatan, dengan penambahan panas, maka fluida diatas plat akan mempunyai viskositas yang lebih rendah, sehingga proses pergerakan fluida lebih cepat, hal ini menyebabkan pergeseran kecepatan, nilai kecepatan lebih tinggi dibandingkan tanpa memakai panas, hambatan pelatpun menjadi lebih kecil, dan perpindahan bentuk aliran dari laminer ke turbulent juga semakin cepat bila dibandingkan dengan kasus 1.

Cara Numerik

langkah-langkah untuk mencari persamaan kecepatan fluida secara numerik adalah
1. melakukan simulasi dengan CFD, detail langkah simulasi
2. Mengambil data nilai kecepatan dan nilai y
3. menghitung regresi linier, dengan program regresi linier yang dibuat sebelumnya, akan didapatkan nilai persamaan ax2+bx+c

untuk mencari persamaan distribusi suhu pada plat, untuk sumbu y dapat dilakukan dengan memasukkan nilai suhu, dan nomor cell arah y, sehingga dengan cara numerik akan didapatkan persamaan distribusi suhu

Proses Simulasi
Langkah per langkah simulasi, hasil serta data yang digunakan dapat dilihat pada file presentasi dibawah ini, saya sengaja menjadikan satu printscreen file simulasi CFDSOFT untuk mempermudahkan pembelajaran selanjutnya, file ini juga bisa didwonload maupun di share, agar file berikut terlihat jelas, disarankan untuk mengklik tombol full view pada kanan bawah



Hasil yang Patut diperhatikan adalah
1. Distribusi Temperature
dapat dilihat terjadi pergeseran bila dibandingkan dengan tanpa adanya penambahan panas pada plat, suhu akan semakin rendah menjauhi dengan permukaan kontak, namun seiring dengan perubahan kecepatan aliran suhu pada x terjauh juga meningkat.

2.Heat Flux, bagian plat yang dekat dengan aliran panas akan mendapatkan heat flux yang lebih besar jika dibandingkan dengan bagian yang jauh dari permukaan, karena pada daerah permukaan kontak terjadi berbegai macam jenis perubahan fisika, pada daerah ini disarankan untuk mengatur jumlah cell sebanyak mungkin agar distribusi perubahan fisika yang terjadi dapat terekam dengan baik,

 Mendapatkan Fungsi Temperature

cara untuk mendapatkan fungsi temperature sama dengan cara mendapatkan fungsi pada kecepatan, lihat lebih jelas di
http://bloghasnan.blogspot.com/2012/04/fungsi-profil-kecepatan-aliran-laminar.html
hanya saja yang data yang dimasukkan berbeda, yaitu data temperature dan data arah y, dari dua data tersebut akan didapatkan hubungan regresi polinomialnya
saya ambil contoh untuk node ke 6, dengan data sebagai berikut

setelah node ke 25 ke atas, nilai suhunya adalah konstan, saya hanya mengambil data sampai dengan node 25, lalu untuk mempermudahkan perhitungan program yang sudah ada, saya modif sebagai berikut
----------
dim A As Double
    Dim b, c, d, e, f, a0, b0, c3, c4, c5, j3, j4, j5 As Double
    For i = 1 To 25
        A = A + Cells(1 + i, 10) ' jumlah total x
        b = b + Cells(1 + i, 11) ' jumlah total y
        c = Cells(1 + i, 10) ^ 2 ' menulis pangkat
-------
sehingga program tersebut hanya membaca sampai dengan data ke 25

Next
        Cells(27, 10) = A
        Cells(27, 11) = b
        Cells(27, 12) = d
        Cells(27, 13) = j3
        Cells(27, 14) = j4
        Cells(27, 15) = f
        Cells(27, 16) = j5
untuk memperdah pembacaah hasil, jumlah dari masing-masing nilai x2,x3,x4,xy, x2y, x dan y saya tampilkan pada baris ke 27 semua, sehingga setelah dilakukan proses perhitungan regresi hasilnya seperti berikut

dari data diatas langkah selanjutnya adalah menyusun matrix 3x3, seperti pada gambar dibawah ini

dengan mengklik tombol "hitung koeffisien matrix" akan muncul form seperti berikut, form ini digunakan untuk mencari nilai a,b,c sebagai fungsi polynomial

matrix A, adalah matrix nilai koeffisien, sedangkan Matrix B adalah matrix nilai hasil
selanjutnya nilai a,b,c akan dihitung, Hasilanya adalah

dari hasil perhitungan menggunakan program numerik yang dibuat, dan dibandingkan dengan nilai regresi polynomial excel didapatkan bahwa hasilnya sangat serupa, sehingga program ini digunakan untuk menghitung nilai regresi node lainya,

Cara Analitis

1. Diagram tegangan geser adanya heat flux, hambatan aliran menjadi boundary layer

2. Diagram langkah analisa setelah diberi heat flux (Ts), thermal boundary layer dijadikan sebagai boundary layer

dari dua diagram diatas, dapat diambil kesimpulan, saat ditambahkan proses perpindahan panas, maka proses analisa yang seharunya digunakan adalah
1. Perpindahan kalor
Heat flux menyentuh wall1 diteruskan secara konduksi ke fluida, lalu pada saat Du/dy = 0 transfer panas berlangsung konveksi ke fluida.
Sehingga Proses Perpindahan kalor adalah 
kalor yang diberikan = kalor yang diterima

Q(heat fluk) = Q (konduksi fluida)
Q (konduksi fluida) = kAdeltaT/x
Q (konduksi fluida) = Q (konveksi)
Q (konveksi) = hAdeltaT
kAdeltaT/x =hAdeltaT
Nu = k /x h
Pr = prandlt number adalah perbandingan hidrostatik boundary layer dengan thermal boundary layer
Pr = v / a

Kesimpulan

hasil plot distribusi temperature pada node x dan arah y menunjukkan, bahwa hasil simulasi yang dihitung dengan numerik, sama dengan hasil analitis (lihat diagram).
 
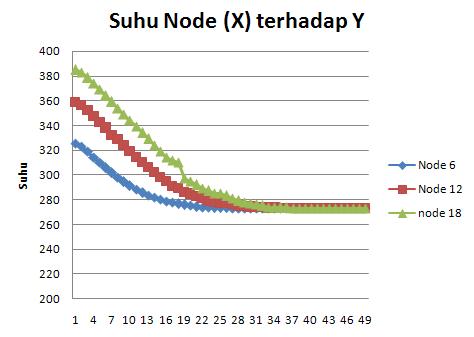
dari Node 6 sampai Node 18, semakin besar arah X maka semakin besar pula suhu yang dihasilkan, hal ini terjadi karena ada kecepatan fluida yang mengarah ke arah x, sehingga semakin besar x maka nilai suhu yang dihasilkan juga semakin besar, begitu juga dengan arah Y, dekat dengan sumber panas (1-7) maka suhu yang dihasilkan juga tinggi, semakin mejauhi lapisan kontak, semakin kecil suhu yang terjadi hingga akhirnya suhu yang dihasilkan konstan.

Read More

Menghitung Hambatan fluida Berdasarkan data, UTS No 2

hambatan pelat ditentukan oleh viskositas, kecepatn profil dan jarak dari permukaan kontak, sehingga secara numerik untuk menentukan nilai hambatan pelat didapatkan dari turunan V searah y (tinggi) dikalikan dengan nilai viskositasnya.

 Keterangan

u adalah kecepatan profil fluida pada tinggi y
U adalah kecepatan maksimum
y adalah tinggi dari plat datar
δ adalah boundary layer
dengan boundary layer ke arah x adalah

 sehingga tergantung dari boundary layernya, aliran dapat menjadi turbulent maupun laminer tergantung dari besar reynold number yang diperoleh.

secara numerik, turunan numerik bisa didapatkan dengan metode newton untuk mencari nilai x secara numerik, namun yang dicari disini bukanlah nilai x nya melainkan adalah nilai hambatan belat (fx) nya, sehingga cukup dengan melakukan integrasi dari nilai u, akan didapatkan nilai hambatan pelat

cara simulasi dan data yang diperoleh dari hasil simulasi adalah sebagai berikut, silahkan lihat di slide presentasi dibawah ini, klik file presentasi nya lalu gerakkan mouse pointer untuk melihat slide berikutnya
data yang terpenting adalah data profil kecepatan sumbu y

 

 ok, sebagai contoh saya ambil untuk node 18 dengan persamaan fungsi kecepatan U nya adalah

-1.1685X2+0.000433X-0.0000688 = Y

maka turunannya adalah

Y' = -2.33X+0.000433

bila diketahui

Panjang plat laminar adalah x = 0.14 meter

dan viskositasnya adalah 9 x 10^-4 kg.m/s

fungsi hambatan fluidanya adalah

F = (9 x 10^-4) x (- 2.33 x (0.14) + 0.000433)

F=  -2.9319x10-4

Read More

Fungsi profil kecepatan aliran laminar pada setiap jarak X, UTS NO 1

Secara numerik tentukan fungsi profil kecepatan aliran laminar pada setiap jarak X dari ujung pelat bagian depan (aliran hulu). Bandingkan dengan hasil analitis ?

penyelesaian untuk mendapatkan data menggunakan CFDSOFT lumayan menyita waktu, proses simulasi pun harus dikerjakan secara bersamaan agar hasil yang didapat lebih cepat, ditambah seringnya problem terhadap koneksi, pengambilan data yang saya gunakan pada pembasan UTS ini dilakukan bersama-sama dengan Almer Ibnu, Irawan, Helmi (yang ternyata tetangga kampung halaman), Gery, dan teman-teman lainya. ok penyelesaian untuk nomer satu kurang lebih sebagai berikut : 

Langkah untuk menentukan Profil Kecepatan secara numerik
sebelumnya saya sudah membuat program untuk menghitung gaus jordan, yaitu untuk menyelesaikan persamaan simultan linier, berikut linknya
http://bloghasnan.blogspot.com/2012/03/penyelesaian-persamaan-simultan.html
program ini akan saya panggil untuk menyelesaikan sistem persamaan linier 3 persamaan yang didapat dari regresi polinomial, penjelasan untuk pemrograman sistem regresi polinomial akan saya sampaikan di bawah ini, sedangkan contoh dari penyelesaian persamaan simulatan dapat dilihat pada link berikut
http://bloghasnan.blogspot.com/2012/03/contoh-hasil-persamaan-simultan-gaus.html
oke, jadi saya rasa bagaimana cara menyelesaikan persamaan simulatan sudah jelas khan, karena untuk mendapatkan nilai regresi ax2+bx+c ya harus memahami metode ini terlebih dahulu.

berikut urutan langkahnya secara numerik
1.  membuat simulasi CFDSOFT atau mengambil data secara langsung, untuk memudahkan pengambilan data dilakukan secara simulasi dari cfdsof
2. dari data CFDSOFT perlu dibuat list untuk dibuat regresi
4. menentukan nilai x dan f(x)
5. menghitung regresi polynomial
Alogaritma regresi polinomial
1. masukkan jumlah n data
1. masukkan data x
2. masukkan data fx
3. For i = 1 To 50
4.       A= A + i
5.       b = b + i
6        c = i ^ 2
7       Cells i = c
8       d = d +i
9       c3 = i ^ 3
10        Cells i = c3
11        j3 = j3 +  i
12        c4 =  i ^ 4
13        Cells i = c4
14       j4 = j4 +  i
15        e = x i * fx i '
16       Cells(1 + i, n) = e 
17        f = f + Cells(1 + i, 15)
18      c5 = (Cells(1 + i, 10) ^ 2)
19       Cells(1 + i, 16) = c5
 20      j5 = j5 + Cells(1 + i, 16)
 21  Next, menulias hasil
 22       Cells(55, 10) = A
 23       Cells(55, 11) = b
 24       Cells(55, 12) = d
 25       Cells(55, 13) = j3
 26       Cells(55, 14) = j4
 27       Cells(55, 15) = f
 28       Cells(55, 16) = j5
sehingga didapatkan nilai matrix 3 x 3 dengan eleminasi gaus akan didapatkan nilai ax2+bx+c

Program Lengkap VBA untuk Regresi Polinomial

Private Sub CommandButton1_Click()
Dim A As Double
    Dim b, c, d, e, f, a0, b0, c3, c4, c5, j3, j4, j5 As Double
    For i = 1 To 50
        A = A + Cells(1 + i, 10) ' jumlah total x
        b = b + Cells(1 + i, 11) ' jumlah total y
        c = Cells(1 + i, 10) ^ 2 ' menulis pangkat
        Cells(1 + i, 12) = c
        d = d + Cells(1 + i, 12) ' jumlah x2
       
        c3 = Cells(1 + i, 10) ^ 3 ' menulis pangkat 3
        Cells(1 + i, 13) = c3
        j3 = j3 + Cells(1 + i, 13) ' jumlah pangkat 3
       
        c4 = Cells(1 + i, 10) ^ 4 ' menulis pangkat 4
        Cells(1 + i, 14) = c4
        j4 = j4 + Cells(1 + i, 14)
               
        e = Cells(1 + i, 10) * Cells(1 + i, 11) ' x kali y
        Cells(1 + i, 15) = e    ' menuliskan nilai x*y
        f = f + Cells(1 + i, 15) ' jumlah xy
       
        c5 = (Cells(1 + i, 10) ^ 2) * Cells(1 + i, 11) ' x*y
        Cells(1 + i, 16) = c5
        j5 = j5 + Cells(1 + i, 16) ' jumlah x2y
       
    Next ' menulis hasil
        Cells(55, 10) = A
        Cells(55, 11) = b
        Cells(55, 12) = d
        Cells(55, 13) = j3
        Cells(55, 14) = j4
        Cells(55, 15) = f
        Cells(55, 16) = j5

 Hasil Program Excel VBA

hasil program yang dibuat merupakan gabungan antara program regresi polynomial dengan program gauss jordan untuk menghitung koeffisien persamaan linier

Urutan langkahnya adalah
1. memasukkan data x dan fx
2. menghitung x2, x3, x4,xy dan x2y
3. menjumlahkan x2, x3, x4,xy dan x2y
4. menyusun persamaan matrix 3x3
5. menghitung koeffsien matrix 3x3
6. menulis hasil koeffisien matrix dalam ax2+bx+c

detailnya adalah seperti berikut
1. memasukkan data x dan fx

 2. data akan otomatis dihitung, pada program ini saya membatasi sampai 50 data, lihat program diatas
 For i = 1 To 50
3. selain itu hasil penjumlahannya juga langsung dhitung dan diletakkan pada cell baris ke 55
next
        Cells(55, 10) = A
        Cells(55, 11) = b
        Cells(55, 12) = d
        Cells(55, 13) = j3
        Cells(55, 14) = j4
        Cells(55, 15) = f
        Cells(55, 16) = j5

4. menyusun persamaan matrix

5. menghitung nilai a,b,c dapat dilakukan dengan mengklik tombol "hitung koeffisien matrix", cara detail lihat posting saya sebelumnya di http://bloghasnan.blogspot.com/2012/03/penyelesaian-persamaan-simultan.html
hasilnya adalah inverse matrix dan nilai koeffisien a,b,c

6. sehingga otomatis nilai dari regresi polynomialnya adalah -3,9x2+0x-0.001

Program Untuk Menghitung Gauss Jordan

membuat modul fungsi yang bisa dipanggil sudah saya jelaskan di beberapa posting sebelumnya, tentang bisection dan newton rapshon,
isi dari module tersebut kira-kira seperti ini, kata garis miring adalah keteranganya, biar mudah dipahami sesuai dengan permintaan sohib-sohib sekelas


Function Gauss_Jordan(A As Variant) As Variant
Dim i As Long, j As Long, k As Long, Atemp
Dim cols As Long, rows As Long, MaxVal As Double
Dim Max_Ind As Double, temp As Double, hold()


    'bila fungsi mulai dipanggil, jumlah kolom dan baris akan dihitung untuk menentukan jumlah n, dan apakah matrix yang ada dapat dihitung, object(A) maksudnya adalah matrix untuk X, = trus artinya bila ada nilainya
 
  If IsObject(A) = True Then
        cols = A.Columns.Count
        rows = A.rows.Count
    Else
        cols = UBound(A, 2)
        rows = UBound(A, 1)
    End If
 
    'menambahkan kolom untuk meletakkan hasil perhitungan,  Atemp merupakan matrix temporary sebelum digunakan nantinya dalam perhitungan.


    cols = cols + cols
    ReDim hold(1 To rows, 1 To cols), Atemp(1 To rows, 1 To cols)
 
    'menambahkan matrix x dan matrix y menjadi augmented matrix, aug matrix adalah matrix gabungan antara x dan y


    For i = 1 To rows
        For j = 1 To rows
            Atemp(i, j) = A(i, j)
            Atemp(i, j + rows) = 0#
        Next j
        Atemp(i, i + rows) = 1#
    Next i
 
    For i = 1 To rows
 
        MaxVal = Atemp(i, i)
        Max_Ind = i
     
 ' prosedure pendek menghitung nilai maximum, hal ini berguna untuk menentukan apakah matirx tersebut ada penyelesaianya atau tidak, akan muncul msg box error bila matrix ternyata singular


        For j = i + 1 To rows
            If Abs(Atemp(j, i)) > Abs(MaxVal) Then
                MaxVal = Atemp(j, i)
                Max_Ind = j
            End If
        Next j
     
        If MaxVal = 0 Then
            MsgBox Prompt:="Matrix adalah singular!", Title:="Error"
            Exit Function
        End If
     
        'prosedure perhitungan pivoting pada matrix


        For j = i To cols
            temp = Atemp(i, j)
                    Atemp(i, j) = Atemp(Max_Ind, j) / MaxVal
                      If Max_Ind <> i Then Atemp(Max_Ind, j) = temp
        Next j
     
     
        For k = 1 To rows
            If k <> i Then          
           
                For j = 1 To cols
                    hold(k, j) = -Atemp(k, i) * Atemp(i, j)
                Next j
           
                For j = 1 To cols
                   Atemp(k, j) = Atemp(k, j) + hold(k, j)
                Next j
            End If
        Next k
    Next i
    Gauss_Jordan = Atemp
End Function

------------------------------------------------------------------------
wahh.. panjang dan ribet? betul sekali, kok bisa bikin program seperti itu? nanti saya tunjukin rahasianya, sekarang kita teruskan membuat programnya

3. program pada button Hitung
double klik tombol hitung lalu masukkan perintah seperti berikut


Private Sub OK_Btn_Click()


Dim i As Double, j As Double, Data As Variant, n As Double
Dim A As Variant, MaxCol As Double, temp As Double, b()
Dim wks, cntsheets, newsheet As Worksheet, FinalCol As Double
Dim x(), Aplus(), Ainv()

' untuk menjaga agar inputan tidak salah, gunakan coding berikut ini, bila input matrix salah, atau ada huruf yang dimasukkan ke dalam cell, maka akan muncul peringatan kalau input matrix salah


If IP_A.Value = Empty Then
        Me.Hide
        MsgBox Prompt:="Pilih Cell untuk memasukkan angka." & vbCr & _
                       "Jangan tulis dengan variablenya.", _
                       Buttons:=48, Title:="Matrix input salah!"
        Me.Show
        Exit Sub
    End If

' matrix A adalah matrix input pada x


A = Application.RANGE(IP_A.Value)
 n = UBound(A, 1)

' pengecekan matrix untuk Y atau B pada program berikut


If IP_b.Value <> Empty Then
        b = Application.RANGE(IP_b.Value)
        If UBound(A, 1) <> UBound(b, 1) Then
            Me.Hide
            MsgBox Prompt:="baris di A harus sama dengan baris di b.", _
                   Buttons:=544, Title:="Error!"

     Err.Description = "Jumlah Baris Matrix tidak sama."
            GoTo EndProc
        End If
    End If' terakhir menghitung inverse yang dilanjutkan untuk menghitung adjoint matrix, sehingga didapatkan nilai x1-xn

Aplus = Gauss_Jordan(A)
        If IsError(Aplus) Then GoTo EndProc
        ReDim Ainv(1 To n, 1 To n)
    For i = 1 To n
        For j = 1 To n
            Ainv(i, j) = Aplus(i, j + n)
        Next j
    Next i

If IP_b.Value <> Empty Then
        x = Application.MMult(Ainv, b)
    End If' hasilnya diletakkan pada sheet baru


   cntsheets = Application.Sheets.Count - Application.Charts.Count
        Set newsheet = Application.Worksheets.add(after:=Worksheets(cntsheets))
        newsheet.name = "Hasil X!"
        FinalCol = 0


With Application
          .Cells(1, FinalCol + 1) = "Inverse Matrix "
        For j = 1 To n
           For i = 1 To n
               .Cells(i + 1, FinalCol + j).Value = Ainv(i, j)
           Next i
        Next j
        If IP_b.Value <> Empty Then
            FinalCol = FinalCol + n
            Cells(1, FinalCol + 1) = "SOLUSI"
            For i = 1 To n
                .Cells(i + 1, FinalCol + 1).Value = x(i, 1)
            Next i
        End If
    End With
 
    Application.Calculation = xlCalculationAutomatic


Unload Me
Exit Sub


Simulasi CFD
langkah untuk simulasi CFD sebenarnya juga sudah dijelaskan pada posting-posting sebelumnya, yang membedakan untuk kasus ini adalah aliran terjadi pada plat tunggal, atau single plate, sehingga untuk menentukan boundary , cell dsb perlu juga diperhatikan, ok, langkah perlangkah untuk simulasi sudah saya buatkan power pointnya di embed object berikut, anda bisa mendownloadnya langsung maupun menshare ke yang lainya. untuk melihatnya pastikan flash player sudah terinstal di bowser anda



Perbandingan Numerik Dan Analisis

hasil simulasi distribusi kecepatan U

Hasil Perbandingan

berikut saya sampaikan beberapa hasil perbandingan antara hasil simulasi dengan numerik
1. contoh pada node 18, dapat dilihat bahwa program yang sudah dibuat menghasilkan nilai regresi yang sama dengan excel, bahkan lebih terliti dengan 6 angka dibelakang koma

dari data diatas dan setelah didapat fungsi profil kecepatan, dan dibuat fungsi regresi linier didapatkan kesimpulan sebagai berikut
a. pada titik x=0 sampai dengan x = 5 kecepatan profilnya membentuk persamaan polynomial
b. antara x = 5 sampai dengan x = 30 aliran yang terjadi adalah laminer, terbukti dengan persamaan kecepatan yang didapat mengarah ke linier.
c. setelah x =31 aliran berubah menjadi turbulent
hal ini sesuai dengan analitis pergerakan fluida pada satu bidang plat datar, bahwa pada x = 0 akan terjadi aliran laminer namun boundary conditionnya bergerak ke atas, sehingga aliran tersebut laminer, selanjutnya aliran tersebut berkembang menjadi turbulent

 gambar diatas merupakan hasil grafik dari beberapa node yang diambil, dari grafik diatas dapat kita lihat perubahan kecepatan ditiap-tiap node, sehingga dapat kita simpulkan bahwa aliran berubah dengan bertambahnya node, semakin tinggi jarak titik terhadap permukaan kontak maka kecepatanya semakin tinggi, hal ini dikarenakan titik yang dekat dengan permukaan kontak akan mengalami gaya tahanan yang lebih tinggi. pada node 30 diperkirakan sudah mencarai full developed region, hal ini dikarenakan nilai regresi yang didapat sudah linier, bukan lagi polynomial.

File lengkap UTS dapat didownload disini

Read More